Bloom Filters for the Perplexed

Discussion on Hacker News.

Bloom filters are one of those simple and handy engineering tools that any engineer should have in their toolbox.

It is a space-efficient probabilistic data structure that represents a set and allows you to test if an element is in it.

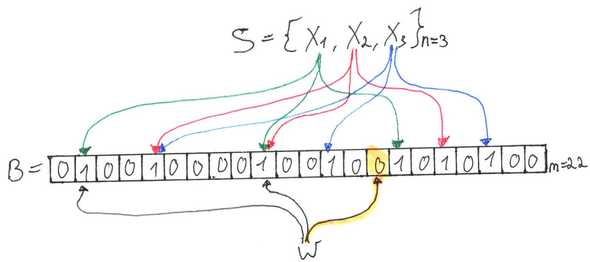
They are really simple to construct and look like this:

The cool thing is that to achieve such space-efficiency Bloom filters allow for errors with an arbitrarily small probability!

Remarkably, a Bloom filter that represents a set of $1$ million items with an error rate of $0.01$ requires only $9585059$ bits ($\text{\textasciitilde}1.14 \text{MB}$)! Irrespective of the length of each element in $S$!

There’re many kinds of Bloom filters. We’ll cover the Standard Bloom Filter as it is the basis for the others and also serves as a nice intro for more advanced probabilistic set-membership data structures such as Cuckoo Filter.

What’s on our menu for today?

• An introduction to standard Bloom filters

  • False Positives and False Negatives
  • Arbitrarily Small Probability of Error (False Positive)
• A python based toy implementation
• Example: Efficiently Verify Compromised SSH Keys

• Applications:

  • Breaking Bitcoin (and Ethereum) Brainwallets
  • Recommender Systems Optimization
  • Search Engine Optimizations
• A derivation of the underlying math for the rusty-engineer :)

All code snippets can be found on Github.

Academic fellows might want to review Bloom’s original $1970$ paper [¹]. Strikingly, Bloom has only $3$ references in his article!

Standard Bloom Filters

A Bloom filter represents a set $S=\{x_1, x_2, \ldots, x_n\}$ of $n$ elements by an array of $m$ bits (initially set to $0$). Lets call it $B$.

A Bloom filter uses $k$ independent hash functions $h_1, \ldots, h_k$ that are assumed to be uniformly distributed over the range $\{1, \ldots, m \}$.

Standard Bloom filters have two operations:

1. Add($x$) - Add $x$ to the Bloom filter.

To represent set $S$ by Bloom filter $B$ we need to Add all $x \in S$.

2. Contains($y$) - Check if $y$ is in the Bloom filter.

To make things clearer, here is a hand-drawn illustration (heavily inspired by Julia Evans (@b0rk) blog illustrations):

False-Negatives and False-Positives

If Contains($y$) returns False, clearly $y$ is not a member of $S$. This property is why we say Bloom filters have zero false-negatives. A situation where Contains($e$) is False and $e \in S$ simply can’t happen (because otherwise all relevant bits were $1$).

If Contains($y$) returns True, $y$ may or may not be a member of $S$. This is why we say that Bloom filters may have false-positives, because a situation where Contains($e$) is True and $e \notin S$ can occur.

Arbitrarily Small Probability of Error (False-Positive)

The cool thing about Bloom filters is that based on $n$ (number of elements in the set $S$) and a chosen probability of false positives $P_{FP}$ we can derive optimal $k$ (number of hash functions) and $m$ (length of bit vector $B$).

These are the formulae (we derive those in the Appendix):

A very cool result is that the optimal number of hash functions $k$ depends only on the false-positive probability $P_{FP}$.

Lets play with it:

import math

def optimal_km(n, p):
  ln2 = math.log(2)
  lnp = math.log(p)
  k = -lnp/ln2
  m = -n*lnp/((ln2)**2)
  return int(math.ceil(k)), int(math.ceil(m))

print(optimal_km(10**6, 0.01)) # Returns (7, 9585059)

Remarkably, a Bloom filter that represents a set of $1$ million items with a false-positive probability of $0.01$ requires only $9585059$ bits ($~1.14 \text{MB}$) and $7$ hash functions. Only $9.6$ bits per element! ($\frac{9585059}{1000000}$).

Toy Implementation

The first thing that comes to mind is how exactly do we get a family of hash functions $h_1, \ldots, h_k$ that are uniformly distributed?

Since our objective is learning and we are not aiming for efficiency, we can simply build our family of hash functions on top of an existing hash function as a primitive. Such as SHA256.

One such construction is the following:

Where:

• $i$ - the number of the hash function.
• $s$ - the string to be hashed.
• $m$ - the length of the bit vector.
• $||$ - string concatenation.

And with Python:

def h_i(i, m, s):
  return int(sha256(bytes([i]) + s).hexdigest(), 16) % m

Recall that the standard bloom filter had two simple operations:

class bloom_filter:
  def __init__(self, m, k, h=h_i):
    self.m = m # length of bit array
    self.k = k # number of hash functions
    self.h = h # hash function
    self.bits = bitarray(self.m) # the actual bit store

  def add(self, s):
    for i in range(self.k):
      self.bits[self.h(i, self.m, s)] = 1

  def contains(self, s):
    for i in range(self.k):
      if self.bits[self.h(i, self.m, s)] == 0:
        return False
    return True # all bits were set

Example: Efficiently Verify Compromised SSH Keys

In 2008, Luciano Bello discovered that Debian’s OpenSSL random number generator was seriously flawed and depended only on a process id integer.

Without getting into the gory details, essentially it means that between 2006 and 2008, cryptographic keys that were generated using OpenSSL on Debian-based operating systems were limited to 32768 different possible keys given their type (e.g. RSA) and size (e.g. 1024 bit).

Fortunately, g0tmi1k (@g0tmi1k), generated all possible compromised keys and uploaded them to a repo.

Say we’d like to build a system that allows users to query whether their keys were compromised.

Moreover say we’d like our system to use a minimal amount of bandwidth and/or requests to the server.

Using a bloom filter for that purpose fits perfectly! Lets see why:

Since Bloom filters have zero false negatives, if key $X$ isn’t in Bloom filter $B$ we know that $X$ isn’t compromised with certainty! Therefore, no more requests needed.

The other case is that $X$ is in $B$:

So a request to verify the state of $X$ must be sent to the server as it may be either a true positive ($X$ is in $B$ and $X$ is compromised) or a false positive ($X$ is in $B$ but $X$ isn’t compromised).

The nice thing about bloom filters is that the size of the Bloom filter is dependent on the false positive probability that is arbitrarily chosen by us!

So if we notice a lot of false positives we can just tune the Bloom filter to our needs and sacrifice some bandwidth for more accuracy.

In Github there’s test_bloom.py which populates a toy Bloom filter with the compromised keys and tests its effectiveness:

$ ./test_bloom.py
[+] Number public keys in ./dsa/1024: 32768. Total length: 19004952 bytes (18.12Mb).
[+] False-positive probability of 0.001.
[+] Optimal number of bits is 471125 (57Kb). 322 times more space efficient.
[+] Optimal number of hash functions is 10.
[+] Test: All public keys were found within the bloom filter.
[+] Test: Average number of false positives: 21, false positive rate: 0.0213. Averaged over 10 tests, 1000 random strings in each test.

Notice that the bloom filter is $322$ more space efficient than the actual length of the public keys (18.12Mb vs. 57Kb)!

If you’d like to run it yourself make sure to follow the simple installation instructions.

For completeness, here’s the code of test_bloom.py:

#!/usr/bin/env python3
`
'''A test script that queries vulnearble keys (debian openssl debacle)
in a space efficient manner using Bloom filters.'''

import glob
import random
from string import ascii_letters
import bloom

def random_string(size=10):
  rand_str = ''.join(([random.choice(ascii_letters) for i in range(size)]))
  return str.encode(rand_str)

def empirical_false_positive_rate(bf, nr_tests=1, nr_strings=1000):
  c = 0
  for i in range(nr_tests):
    rand_strings = [random_string(30) for i in range(nr_strings)]
    t = 0
    for r in rand_strings:
      if bf.contains(r):
        t += 1
    c += t
  avg_fpr = ((c/nr_tests)*(1/nr_strings))
  avg_errs = c/nr_tests
  return (int(avg_errs), avg_fpr)

if __name__ == '__main__':
  public_keys = set()
  total_keys_bytes= 0

  for pk_file in glob.glob('./dsa/1024/*.pub'):
    pk_base64 = open(pk_file, 'rb').read().split()[1]
    total_keys_bytes += len(pk_base64)
    public_keys.add(pk_base64)

  n = len(public_keys)
  print('[+] Number public keys in ./dsa/1024: {}. Total length: {} bytes ({:0.2f}Mb).'.format(n, total_keys_bytes, total_keys_bytes/(2**20)))

  p = 1/1000
  print('[+] False-positive probability of {}.'.format(p))

  k, m = bloom.optimal_km(n, p)
  t = int((total_keys_bytes*8)/m)
  print('[+] Optimal number of bits is {} ({}Kb). {} times more space efficient.'.format(m, int(m/(8*(2**10))), t))
  print('[+] Optimal number of hash functions is {}.'.format(k))

  # Populating our bloom filter.
  bf = bloom.bloom_filter(m, k)
  for pk in public_keys:
    bf.add(pk)

  # Testing that all public keys are inside the bloom filter
  all_pks_in_bf = True
  for pk in public_keys:
    if not bf.contains(pk):
      all_pks_in_bf = False
      break

  if all_pks_in_bf:
    print('[+] Test: All public keys were found within the bloom filter.')
  else:
    # Can't be...
    print('[-] Test: One or more public key were not found within the bloom filter.')

  # Testing the empirical false positive rate by generating random strings
  # (that are surely not in the bloom filter) and check if the bloom filter
  # contains them.
  nr_tests = 10
  nr_strings = 1000
  avg_errs, avg_fpr = empirical_false_positive_rate(bf, nr_tests, nr_strings)
  print('[+] Test: Average number of false positives: {}, false positive rate: {:0.4f}. Averaged over {} tests, {} random strings in each test.'.format(avg_errs, avg_fpr, nr_tests, nr_strings))

Applications

In their 1994 paper, Andrei Broder and Michael Mitzenmacher coined the Bloom Filter Principle:

Wherever a list or set is used, and space is at a premium, consider using a Bloom filter if the effect of false positives can be mitigated.

Andrei Broder and Michael Mitzenmacher

Below are some cool applications I’ve bumped into over the years.

Breaking Bitcoin (and Ethereum) Brainwallets

In DEFCON 23 (2015), Ryan Castellucci (@ryancdotorg) presented Brainflayer. A cryptocurrency brainwallet cracker that uses a Bloom filter under the hood.

I specifically abstracted away low level Bitcoin technicalities.

Bitcoin’s blockchain is made out of a sequence of blocks. Each block contains transactions and each transaction cryptographically instructs to transfer $X$ Bitcoins from a previous transaction to a Bitcoin address.

How does a Bitcoin address is generated?

A Bitcoin address $A$ is simply a hashed ECDSA public-key $Q$. Lets denote $A = H(Q)$.

How does an ECDSA public key is generated?

An ECDSA public key $Q$ is the outcome of multiplying a private key $d$ with some known constant base point $G$. That is, $Q = d \times G$.

How does an ECDSA private key is generated?

An ECDSA private key $d$ is simply an integer that is preferably generated using a cryptographically secure random number generator. Anyone that knows $d$ can redeem Bitcoins that were sent to $A$.

What’s a Brainwallet address?

A Brainwallet is simply a Bitcoin address where its corresponding private key $d$ was generated using a mnemonic (!) rather then a secure random number generator. One possible Brainwallet construction looks like:

For instance, the string (embedded in Bitcoin’s Genesis block):

The Times 03/Jan/2009 Chancellor on brink of second bailout for banks

When hashed with SHA256 yields the following ECDSA private key:

a6d72baa3db900b03e70df880e503e9164013b4d9a470853edc115776323a098

That yields the following Bitcoin address:

1Nbm3JoDpwS4HRw9WmHaKGAzaeSKXoQ6Ej

Using a blockchain explorer we can check the address’s history and see that it was used :)

Using a Bloom filter to crack Brainwallets

It is rather straight forward:

1. Extract all Bitcoin addresses from the Blockchain.
2. Add them to a Bloom filter $B$.
3. Generate a set $W$ of Bitcoin addresses using plausible mnemonics (“Brainwallets”).
4. Gather possible candidates set $C$ - addresses from $W$ that $B$ returns positive on.
5. Filter out false positives by checking which addresses in $C$ exist on the Blockchain.

Currently, Bitcoin’s blockchain contains about $440M$ unique addresses (according to Quandl - press on Cumulative).

Ryan’s implenetation contains a bloom filter of length $512MB$ and $20$ hash functions (he actually uses simple functions over the original public key hashes - no heavy cryptographic hash - neat).

In the Appendix we derived an experssion for the false positive probability:

Where $k$ is the number of hash functions, $n$ the length of the set and $m$ the length of the bloom filter.

def exact_pfp(n, m, k):
  return ( 1 - (1 - (1/m))**(k*n) )**k

m_bytes = 512*1024*1024
m_bits = m_bytes * 8
k = 20

print(exact_pfp(440*(10**6), m_bits, k)) # ~0.063
print(exact_pfp(220*(10**6), m_bits, k)) # ~0.000137
print(exact_pfp(110*(10**6), m_bits, k)) # ~1.14e-08
print(exact_pfp(80*(10**6), m_bits, k))  # ~7.16e-11

As one can tell from above, a Bloom filter of length $512MB$ and $20$ hash functions has a high false positive rate on $440M$ items.

In 2015, when Ryan released Brainflayer, there were about $80M$ unique addresses on the blockchain and such a construction yielded a very low false postive rate of $\sim 7.16\times 10^{-11}$.

Today, in order to maintain a similar false positive rate, one would have to either dissect the blockchain to chunks and use several Bloom filters of length $512MB$, or simply increase the length of the bloom filter and the number of hash functions.

I highly recommened you to go and watch Ryan’s talk.

Recommender System Optimization

Simply put, a recommender system $R$ is an algorithm that predicts the preferences of a user.

For instance, you’ve just bought The Hard Thing About Hard Things. Amazon’s recommender system learns that you like books about entrepreneurship and start show you other book recommendations.

But, how do you keep track of irrelevant recommendations such as books the user already read or dismissed ?

Say $X$ books were recommended by $R$. $X$ is comprised of $Y$ relevant and $Z$ irrelevant recommendations ($Y \cap Z = \emptyset$).

Using a Bloom filter $B_Z$ to store irrelevant recommendations $Z$ is one possible answer.

First, say we’re dealing with a lot of irrelevant recommendations, then since Bloom filters are space efficient, it reduces the data stored per user substantially, and even bandwidth (if your logic resides in client side).

Second, since Bloom filters have zero false-negatives, we are guarunteed that a user will never be shown irrelevant recommendations (the event where $e \in Z$ and $B_{Z}.contains(e)$ is false can’t happen).

Third, since Bloom filters may have false-positives, a relevant recommendation may not be shown to the user (the event where $e \in Y$ and $B_{Z}.contains(e)$ is true). But that’s ok since nothing will happen if a user won’t get a relevant recommendation once every 1K visits.

I’d like to thank Sébastien Bratières for spotting an error in this clause.

Search Engine Optimizations

In his 2016 Strange Loop talk, Dan Luu (@danluu), shared some of the internals of one of Bing’s production search indices: BitFunnel (hint: they use Bloom filters, but not in a trivial way).

The talk is short and built in a very constructive way:

You might want to review BitFunnel’s SIGIR’17 paper.

Appendix

While studying the math behind Bloom filters I found myself rusty and confused. Here is a guided tour for the rusty-confused engineer :)

False-Positive Probability and Formulae

Assume Bloom filter $B$ was populated with elements from $S$.

A false-positive is an input $y$ that isn’t an element of $S$ but $B[h_1(y)], \ldots, B[h_k(y)]$ are all set to $1$.

The false-positive probability $P_{FP}$ then is simply the probability of having any $k$ arbitrary cells set to $1$ after Bloom filter $B$ is populated with elements from $S$.

Lets define $P_1$ to be the probability that a certain bit is set to $1$ after we populate the Bloom filter.

Given $P_1$, the probability of a false positive, $P_{FP}$ is simply:

But, how do we calculate $P_{1}$ ?

Lets assume now that Bloom filter $B$ is empty and we begin add elements from $S$.

Given $x_1$ we compute $h_1(x_1)$ and set $B[h_1(x_1)]$ to $1$. What’s $P_1$ now?

because we assume $h_i$ are uniform over $\{1, \ldots, m\}$.

Next, we compute $h_2(x_1)$ and set $B[h_2(x_1)]$ to $1$. What’s $P_1$ now?

Wait! Why did you subtract $\frac{1}{m^2}$ ?

Recall that we defined $P_1$ to be the probability that a specific bit is set to $1$. This specific bit might be set to $1$ by either $h_1$ or $h_2$ or both. That is, we search for the probability of the union of independent events that are not mutually exclusive.

We subtract $\frac{1}{m^2}$, since otherwise we “count” the event that both $h_1$ and $h_2$ set the bit to $1$ twice. This is due to the Inclusion-Exclusion Principle.

Doing the same thing for $h_3$. What’s $P_1$ now?

As evident from above, if we continue this way we end up with a rather intricate expression for $P_1$. For this reason, most derivations of the false-positive probability use the complementary event to go around it.

Lets define $P_0$ to be the probability that a certain bit is not set to $1$.

If we knew $P_0$ we could easily compute $P_1$ and $P_{FP}$:

So, how do we calculate $P_{0}$ ?

Lets start with an empty Bloom filter $B$ again and add elements from $S$.

Given $x_1$ we compute $h_1(x_1)$ and set $B[h_1(x_1)]$ to $1$. What’s $P_0$ now?

Next, we compute $h_2(x_1)$ and set $B[h_2(x_1)]$ to $1$. What’s $P_0$ now?

Wait! Why does $P_1$ and $P_0$ differ at this stage of the analysis?

Because when calculating $P1$ we wanted the probability of the event that at least one of the hash functions sets a specific bit. But, for $P_0$ we want the probability that all hash functions does not set a specific bit!

That is, we search for the probability of the intersection of independent events that are not mutually exclusive.

Setting the bits for the other hash functions $h_3(x_1), h_4(x_1), \ldots, h_k(x_1)$:

And since we add $n$ elements:

Therefore:

Since we want to find the optimal $k$ and $m$ such that $P_{FP}$ (the false probably rate) is minimized, we will need to differentiate it.

The expression for $P_{FP}$ isn’t easy to differentiate, this is why most derivations use a neat trick that represents it with $e$ (Euler’s number).

One of $e$’s many definitions is:

That is, for large enough $n$, $e$ is approximately $\left( 1 + \frac{1}{n}\right)^n$.

Therefore,

Hence, $P_{FP}$ can be reduced to the following expression:

Although we got a nicer expression for $P_{FP}$, we would like to differentiate it with respect to $k$ (to find the the optimal number of hash functions). But $k$ is the exponent.

To differentiate such equations usually one uses some $\ln$ (natural logarithm) trickery.

For any function $f(x,y) = g(y)^{x}$ ($g$ is simply a function of $y$) it holds that:

Therefore, in the case of our $P_{FP}$:

Lets denote $g = k \cdot ln(\left(1 - e^{\frac{kn}{-m}}\right))$, which makes $P_{FP} = e^{g}$.

Since $e$ is a monotonically increasing function minimizing $e^{g}$ is equivalent to minimizing $g$ with respect to $k$.

Differentiating $g$ with respect to $k$ (WolframAlpha):

To find the optimal $k$, the one that minimizes the above expression, one needs to equate it to $0$

It is easy to verify that the derivative is $0$ when $k=ln 2 \cdot \frac{m}{n}$:

Great! Now we know that $k=ln 2 \cdot \frac{m}{n}$ is the optimal number of needed hash functions.

A very cool result of bloom filters is that $k$ only depends on a given $P_{FP}$.

To achieve that result, lets plug the $k$ we got in equation we derived for the false positive probability:

Taking $ln$ on both sides:

Therefore, $m$, the number of bits in our bloom filter (number of bits in $B$) is:

Pluggin that $m$ into the $k$ we got yields:

And voila, $k$ depends only on a given false positive probability $P_{FP}$!

Summary

Bloom filters are simple and useful beasts. They were designed in times of great scarcity in memory, but since nowadays we explode in data they fit almost perfectly for our times as well!

If you found this article interesting, make sure to read about Scalable Bloom filters which allows you to add items to an already existing Bloom filter and Counting Bloom filters which allows you to delete items from an already existing Bloom filter.

If you spot an error / have any question please let me know so others may gain :)

Comments and thoughts are also welcome on this tweet:

Bloom Filters for the Perplexed! https://t.co/LCzadJGhlh

— Sagi Kedmi (@SagiKedmi) September 27, 2017